Scottish household survey 2015: annual report
Report presenting reliable and up-to-date information on the composition, characteristics and behaviour of Scottish households.
Annex 3: Confidence Intervals and Statistical SignificanceThe Representativeness of the Scottish Household Survey
Although the Scottish Household Survey ( SHS) sample is chosen at random, the people who take part in the survey will not necessarily be a representative cross-section of the population. Like all sample surveys, the results of the SHS are estimates for the whole population and these results might vary from the true values in the population for three main reasons:
1. The sample frame does not completely cover the population because accommodation in hospitals, prisons, military bases, larger student halls etc. are excluded from the sampling frame. The SHS provides a sample of private households rather than all households. The effect of this on the representativeness of the data is not known.
2. Some people refuse to take part in the survey and some cannot be contacted by interviewers. If these people are systematically different from the people who are interviewed, this represents a potential source of bias in the data. Comparison of the SHS data with other sources suggests that for the survey as a whole, any bias due to non-response is not significant [92] .
3. Samples always have some natural variability because of the random selection of households and people within households. In some areas where the sample is clustered, the selection of sampling points adds to this variability.
Each of these sources of variability becomes much more important when small sub-samples of the population are examined. For example, a sub-sample with only 100 households might have had very different results if the sampling had, by chance, selected four or five more households with children, rather than households including one or two adults of pensionable age and no younger adults.
Confidence Intervals
The likely extent of sampling variability can be quantified by calculating the 'standard error' associated with an estimate produced from a random sample. Statistical sampling theory states that, on average:
- Only about one sample in three (33 per cent) would produce an estimate that differed from the (unknown) true value by more than one standard error;
- Only about one sample in twenty (5 per cent) would produce an estimate that differed from the true value by more than two standard errors;
- Only about one sample in 400 (0.25 per cent) would produce an estimate that differed from the true value by more than three standard errors.
- By convention, the '95 per cent confidence interval' is defined as the estimate plus or minus about twice the standard error because there is only a 5 per cent chance (on average) that a sample would produce an estimate that differs from the true value of that quantity by more than this amount.
The standard error of the estimate of a percentage depends upon several things:
- The value of the percentage itself;
- The size of the sample (or sub-sample) from which it was calculated ( i.e. the number of sample cases corresponding to 100 per cent per cent);
- The sampling fraction ( i.e. the fraction of the relevant population that is included in the sample); and
- The 'design effect' associated with the way in which the sample was selected (for example, a clustered random sample would be expected to have larger standard errors than a simple random sample of the same size).
Figure A3 1 at the end of this Annex shows the 95 per cent confidence limits for a range of estimates calculated for a range of sample sizes, incorporating a design factor of 1.16 [93] to account for the complex survey design. To estimate the potential variability for an estimate for the survey you should read along the row with the value closest to the estimate until you reach the column for the value closest to the sub-sample. This gives a value which, when added and subtracted from the estimate, gives the range (the 95 per cent confidence interval) within which the true value is likely to lie. Where the exact value is not given in the table, we recommend using the closest value in the table. Otherwise, you may also derive more precise estimates through using standard formulas for confidence intervals from survey estimates, incorporating a design factor of 1.16.
For example, if the survey estimates that 18.0 per cent of households in Scotland are 'single adult' households and this has a confidence interval of ±0.9 per cent, it means that, we could be 95 per cent confident that the true value for the population lies between 17.1 per cent and 18.9 per cent.
However, smaller sample sizes have wider confidence intervals. So, for example, looking at household type might show that in, say, Edinburgh, 28.0 per cent of households are 'single adult' households. However, if there were 780 households in Edinburgh interviewed, this estimate would have a 95 per cent confidence interval of approximately ±3.7 per cent. This suggests that the true value lies between 24.3 per cent and 31.7 per cent. Clearly, the estimate for any single area is less reliable that the estimate for Scotland as a whole.
Statistical Significance
Because the survey's estimates may be affected by sampling errors, apparent differences of a few percentage points between sub-samples may not reflect real differences in the population. It might be that the true values in the population are similar but the random selection of households for the survey has, by chance, produced a sample which gives a high estimate for one sub-sample and a low estimate for the other.
A difference between two areas is significant if it is so large that a difference of that size (or greater) is unlikely to have occurred purely by chance. Conventionally, significance is tested at the 5 per cent level, which means that a difference is considered significant if it would only have occurred once in 20 different samples. Testing significance involves comparing the difference between the two samples with the 95 per cent confidence limits for each of the two estimates.
For example, suppose the survey estimates that there are 14 per cent 'single adult households' in Stirling (±4.1 per cent), 10 per cent in Aberdeenshire (±1.7 per cent), 15 per cent in Fife (±2.0 per cent), and 24 per cent in Edinburgh (±2.5 per cent). Assuming that the estimates' values are 'exact' ( i.e. that the figure underlying 10 per cent is 10.0 per cent), we can say the following:
- The difference between Stirling and Fife is not significant because the difference between the two (1 per cent) is smaller than either of the confidence limits (at least ±2.0 per cent). In general, if the difference is smaller than the larger of the two limits, it could have occurred by chance and is not significant;
- The difference between Stirling and Edinburgh is significant because the difference (10 per cent) is greater than the sum of the limits (4.1 + 2.5 = 6.6 per cent). In general, a difference that is greater than the sum of the limits is significant.
If the difference is greater than the larger of the two confidence limits, but less than the sum of the two limits, the difference might be significant, although the test is more complex.
Statistical sampling theory suggests that the absolute value of the difference between the two estimates 〖(p〗_1-p_2) is significant if it is greater than the square root of the sum of the squares of the limits for the two estimates, as explained by the following formula:
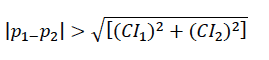
The difference of 5 per cent between Aberdeenshire and Fife is greater than the largest confidence limit (±4.1 per cent) but it is less than the sum of the two limits (4.1 per cent + 2.0 per cent = 6.1 per cent) so it might be significant. In this case 4.12 = 16.81 and 2.02 = 4 giving a total of 20.81. The square root of this is 4.56, which means that the difference of 5 per cent is significant (although only just). Similar calculations will indicate whether or not other pairs of estimates differ significantly.
It should be noted that the estimates published in this report have been rounded, generally to the nearest whole number, and this can affect the apparent significance of some of the results. For example:
- If the estimate for Aberdeenshire was 10.49 per cent (rounded to 10 per cent) and the estimate for the Fife was 14.51 per cent (rounded to 15 per cent) the difference would be calculated as 4.02 per cent rather than 5 per cent. This is below the calculated 'significance threshold' value of 4.56 per cent;
- If, however, the estimate for the Lothians was 10.51 per cent (rounded to 11 per cent) and the estimate for Fife was 15.49 per cent (rounded to 15 per cent) the difference would be calculated as 4.98 per cent rather than 5 per cent. This is higher than 4.56 per cent.
For this reason, caution should be exercised where differences are on the margins of significance. In general, we would suggest that differences should only be considered significant where the difference is clearly beyond the threshold of significance.
Statistical Significance and Representativeness
Calculations of confidence limits and statistical significance only take account of sampling variability. The survey's results could also be affected by non-contact/non-response bias. If the characteristics of the people who should have been in the survey but who could not be contacted, or who refused to take part, differ markedly from those of the people who were interviewed, there might be bias in the estimates. If that is the case, the SHS results will not be representative of the whole population.
Without knowing the true values (for the population as a whole) of some quantities, we cannot be sure about the extent of any such biases in the SHS. However, comparison of SHS results with information from other sources suggests that they are broadly representative of the overall Scottish population, and therefore that any non-contact or non-response biases are not large overall. However, such biases could, of course, be more significant for some sub-groups of the population or in certain council areas, particularly those that have the highest non-response rates.
In addition, because it is a survey of private households, the SHS does not cover some sections of the population - for example, it does not collect information about students in halls of residence. Please refer to the companion technical reports [94] for a comparison of SHS results with information from other sources.
A3 1: Estimated sampling error associated with different proportions for different sample sizes
| 100 | 200 | 300 | 400 | 500 | 700 | 1,000 | 2,000 | 3,000 | 4,000 | 5,000 | 6,000 | 7,000 | 8,000 | 9,000 | 10,000 | 11,000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5% | 4.9% | 3.5% | 2.9% | 2.5% | 2.2% | 1.9% | 1.6% | 1.1% | 0.9% | 0.8% | 0.7% | 0.6% | 0.6% | 0.6% | 0.5% | 0.5% | 0.5% |
| 10% | 6.8% | 4.8% | 3.9% | 3.4% | 3.0% | 2.6% | 2.2% | 1.5% | 1.2% | 1.1% | 1.0% | 0.9% | 0.8% | 0.8% | 0.7% | 0.7% | 0.6% |
| 15% | 8.1% | 5.7% | 4.7% | 4.0% | 3.6% | 3.1% | 2.6% | 1.8% | 1.5% | 1.3% | 1.1% | 1.0% | 1.0% | 0.9% | 0.9% | 0.8% | 0.8% |
| 20% | 9.1% | 6.4% | 5.2% | 4.5% | 4.1% | 3.4% | 2.9% | 2.0% | 1.7% | 1.4% | 1.3% | 1.2% | 1.1% | 1.0% | 1.0% | 0.9% | 0.9% |
| 25% | 9.8% | 6.9% | 5.7% | 4.9% | 4.4% | 3.7% | 3.1% | 2.2% | 1.8% | 1.6% | 1.4% | 1.3% | 1.2% | 1.1% | 1.0% | 1.0% | 0.9% |
| 30% | 10.4% | 7.3% | 6.0% | 5.2% | 4.6% | 3.9% | 3.3% | 2.3% | 1.9% | 1.6% | 1.5% | 1.3% | 1.2% | 1.2% | 1.1% | 1.0% | 1.0% |
| 35% | 10.8% | 7.6% | 6.2% | 5.4% | 4.8% | 4.1% | 3.4% | 2.4% | 2.0% | 1.7% | 1.5% | 1.4% | 1.3% | 1.2% | 1.1% | 1.1% | 1.0% |
| 40% | 11.1% | 7.9% | 6.4% | 5.6% | 5.0% | 4.2% | 3.5% | 2.5% | 2.0% | 1.8% | 1.6% | 1.4% | 1.3% | 1.2% | 1.2% | 1.1% | 1.1% |
| 45% | 11.3% | 8.0% | 6.5% | 5.6% | 5.0% | 4.3% | 3.6% | 2.5% | 2.1% | 1.8% | 1.6% | 1.5% | 1.3% | 1.3% | 1.2% | 1.1% | 1.1% |
| 50% | 11.3% | 8.0% | 6.5% | 5.7% | 5.1% | 4.3% | 3.6% | 2.5% | 2.1% | 1.8% | 1.6% | 1.5% | 1.4% | 1.3% | 1.2% | 1.1% | 1.1% |
| 55% | 11.3% | 8.0% | 6.5% | 5.6% | 5.0% | 4.3% | 3.6% | 2.5% | 2.1% | 1.8% | 1.6% | 1.5% | 1.3% | 1.3% | 1.2% | 1.1% | 1.1% |
| 60% | 11.1% | 7.9% | 6.4% | 5.6% | 5.0% | 4.2% | 3.5% | 2.5% | 2.0% | 1.8% | 1.6% | 1.4% | 1.3% | 1.2% | 1.2% | 1.1% | 1.1% |
| 65% | 10.8% | 7.6% | 6.2% | 5.4% | 4.8% | 4.1% | 3.4% | 2.4% | 2.0% | 1.7% | 1.5% | 1.4% | 1.3% | 1.2% | 1.1% | 1.1% | 1.0% |
| 70% | 10.4% | 7.3% | 6.0% | 5.2% | 4.6% | 3.9% | 3.3% | 2.3% | 1.9% | 1.6% | 1.5% | 1.3% | 1.2% | 1.2% | 1.1% | 1.0% | 1.0% |
| 75% | 9.8% | 6.9% | 5.7% | 4.9% | 4.4% | 3.7% | 3.1% | 2.2% | 1.8% | 1.6% | 1.4% | 1.3% | 1.2% | 1.1% | 1.0% | 1.0% | 0.9% |
| 80% | 9.1% | 6.4% | 5.2% | 4.5% | 4.1% | 3.4% | 2.9% | 2.0% | 1.7% | 1.4% | 1.3% | 1.2% | 1.1% | 1.0% | 1.0% | 0.9% | 0.9% |
| 85% | 8.1% | 5.7% | 4.7% | 4.0% | 3.6% | 3.1% | 2.6% | 1.8% | 1.5% | 1.3% | 1.1% | 1.0% | 1.0% | 0.9% | 0.9% | 0.8% | 0.8% |
| 90% | 6.8% | 4.8% | 3.9% | 3.4% | 3.0% | 2.6% | 2.2% | 1.5% | 1.2% | 1.1% | 1.0% | 0.9% | 0.8% | 0.8% | 0.7% | 0.7% | 0.6% |
| 95% | 4.9% | 3.5% | 2.9% | 2.5% | 2.2% | 1.9% | 1.6% | 1.1% | 0.9% | 0.8% | 0.7% | 0.6% | 0.6% | 0.6% | 0.5% | 0.5% | 0.5% |
Contact
Email: Jackie Horne
There is a problem
Thanks for your feedback