Scottish housing market: tax revenue forecasting models – review
Findings of an independent literature review of tax revenue forecasting models for the housing market.
3. Model assessment
Table 2 lists the broad model classes that we cover. [4] We focus the review on model classes and methods within model classes that are likely to be appropriate for the housing market in Scotland in a public budgeting context.
We start by describing the simple assumptions that many practitioners use in place of elaborate models. These include using a rule of thumb, a growth accounting framework (decomposing the series into its main drivers and projecting them forward mechanically), or a consensus forecast (an average of external non-government forecasters).
We then introduce univariate time series models that predict future values of housing prices and transactions using only the past statistical properties of the series itself. These include models that use the tendency of a series to return to its path following shocks ( ARIMA modelling), models that estimate a series' tendency to behave differently over different periods (regime-switching models), and models that forecast a series' volatility ( GARCH).
Next, we review multivariate econometric models grounded in theoretical relationships between the housing market and other economic drivers (such as employment growth, household incomes, and population). These models attempt to predict both the path of the series and why it will take that path.
We also look at models that combine both time series and multivariate approaches in a multiple equation simultaneously determined framework: the vector autoregression approach.
We follow this with error-correction models, which were created to address technical issues with non-stationary time series data, and large-scale macroeconometric models, which use a combination of techniques to forecast the housing market as a key component of a system of equations for the economy as a whole.
We then look at theory-based models that use optimising agents (micro-foundations) to arrive at a forecast: dynamic stochastic general equilibrium models.
Finally, we assess microsimulation models that use survey data and tax return samples (or sometimes the entire universe of transactions) to build up a complete description of taxpayers in the economy.
Table 2: Assessed model classes
| Description |
Class |
|---|---|
| Assumption or rule based |
Rules of thumb Growth accounting models External consensus forecasts |
| Univariate time-series |
ARIMA GARCH Regime-switching models |
| Multivariate approaches |
Multivariate regression models Vector autoregressive models Error-correction models Large-scale macroeconometric models |
| Theory-based micro-founded |
Dynamic stochastic general equilibrium models |
| Policy-focused models |
Microsimulation models |
3.1 Forecasting by technical assumption
Practitioners often use approaches that are mechanical in nature, requiring little to no judgment or estimation of model parameters. We refer to these methods as technical assumptions. There were three general forms of technical assumptions that appeared frequently in budget backgrounders and practitioner interviews: 1) rules of thumb, 2) growth accounting models, and 3) an average of external forecasts.
Rules of thumb are simple approaches that are grounded in theory, have shown value in practice, or are chosen subjectively because forecasters have judged that it is not worth applying significant modelling effort (for example, if the series is negligible as a percentage of the overall budget or GDP). They can be applied to both prices and transactions. They often resemble techniques in other model classes, with the difference that they generally do not contain estimated parameters or are estimated mechanically. Rules of thumb can take a range of sophistication:
- holding the variable constant in the future based on its last observation
- projecting it forward using its simple historical average (the mean)
- using a constant trend growth assumption (for example, its historical average growth rate)
- using an exponential smoothing model
- a simple one-to-one growth relationship with other economic variables, such as GDP
Holding a variable constant based on its last observation would be appropriate if, for example, examination of the series suggests that it follows no predictable pattern, with long periods trending up or down-that is, it is a random walk. If, however, it seems to fluctuate randomly around a stable value, then it may make sense to use its historical mean, or a moving average (the sample over which the mean is estimated goes back a limited number of periods and moves along as more observations are added). [5] These rules may be appropriate for housing transactions if new housing development is restricted and population, real incomes, and demographics are stable.
Similarly, projecting the series with a constant growth rate could be appropriate if historically prices have grown at roughly the same rate as general CPI price inflation, or for transactions if there are few restrictions on development and population is growing steadily.
Exponential smoothing models resemble a moving average, but values further in the past are given decreasingly smaller weights in its calculation. Exponential smoothing techniques have been developed that can handle trending and seasonal data, and are easily applied in a push-button manner by spreadsheet programs and statistical software. [6]
Rules of thumb could also be based on rough economic relationships, such as assuming the nominal housing tax base grows with the growth of nominal GDP. Growing the tax base with the growth rate of nominal GDP is the same as assuming it grows by population, inflation and real incomes (productivity). Equivalently, this assumes the average consumer will spend the same proportional amount of their income on housing services over time
Rules of thumb can be decided by forecasters using basic descriptive statistics and judgment, or they can be institutionalised to impart a degree of independence by being imposed by an arm's-length body such as the Auditor General for Scotland.
Alternatively, forecasters could use a growth accounting model that decomposes prices and transactions into their main cost drivers. For example, Moro and Nuño (2012) assume that average house prices in a period ( P t,) are directly related to construction costs. They decompose costs into the cost of capital (the interest rate on borrowing, R t) and the cost of labour (the wage rate, W t) in the construction sector relative to the rest of the economy, using a growth equation like the following: [7]
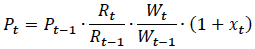
where x t is a residual growth factor capturing growth in excess of capital and labour costs. All variables are expressed as a ratio of prices in the construction sector to prices in the general economy.
This framework can be used to project housing prices using forecasts taken from a macroeconomic model for R t and W t. Practitioners typically hold future values of x t constant at its historical average, unless there is a strong reason to suspect otherwise. Accounting methods incorporate economic drivers, but often assume away business cycle considerations (such as short-run deviations of supply and demand from equilibrium). For this reason, they are generally referred to as projections rather than forecasts (Belsky, Drew, and McCue (2007) discuss this distinction). Accounting projections are nonetheless common in forecasting frameworks reported by practitioners, especially when the series is volatile and difficult to predict, or for projections beyond five years (for example, as part of long-term debt sustainability projections that assume markets are in equilibrium).
Finally, the Scottish forecasting framework could use an average of non-government forecasts. This would involve regularly surveying private sector banks, real estate industry firms and experts, think tanks, and universities for their outlook for the housing market. The individual forecasts would then be combined using a simple average for each year of the forecast. If not used to generate the housing market forecast itself, the survey could be used to generate exogenous economic assumptions for more sophisticated models.
Assessment
Application (forecasting): good. Examples of rules of thumb come mostly from practitioner literature and interviews. Prior to the creation of the Office for Budget Responsibility ( OBR), the UK budget was prepared in part by using a set of basic assumptions audited by the National Audit Office, including assumptions for trend GDP growth, unemployment, equity prices, oil prices, and tobacco consumption trends. [8]
The OBR uses a rule of thumb for its forecasts of the devolved Scottish LBTT and Welsh SDLT taxes, assuming they remain at a constant share of their forecast for the UK as a whole ( OBR, 2016).
Practitioners reported that assuming a constant share of GDP is the "go-to" assumption for small taxes, or taxes for which data on fundamentals is limited.
The Scottish Government forecast housing prices in Draft Budget 2016-17 using a rule of thumb for the outer years of the outlook, interpolating between model results after the second year of the outlook to the historical average growth rate for prices in the fifth year. For transactions, the Scottish Government used a linear interpolation rule of thumb between the last historical value of the turnover rate to the historical average turnover rate imposed on the fifth year of the forecast horizon.
A growth accounting framework is used to project medium-run demand for homes based on fundamentals by the Joint Center for Housing Studies of Harvard University and presented most recently in Belsky et al. (2007). This approach models US housing demand with a simple accounting relationship based on three factors: 1) net household growth (itself projected using headship rates and immigration), 2) the net change in vacant units (calculated with demand for for-sale vacancies, for-rent vacancies, and second and occasional use homes-in turn projected by the age distribution of population, household wealth, and preferences), and 3) replacement of units lost on net from existing stock as a result of disaster, deterioration, demolition, and conversion to non-residential units. Although the framework is for new home construction, it could be extended to include turnover for existing homes for a projection of total transactions.
Belsky et al. also present an alternative and simpler approach to projecting total demand for new housing using the historical ratio of household growth to completions (the two most reliable housing data sources according to the authors).
If short-run dynamics are desired, McCue (2009) provides an extension of the Belsky et al. framework to compare the demand projections to actual supply to arrive at a short-run forecast of excess new supply and inventories. This excess (or deficit) supply measure could be used to introduce short-run cyclicality in prices using a multivariate regression model (discussed further in Subsection 3.3) while still being anchored at the end of the medium run by the accounting framework.
Growth accounting models may, however, be less suited to forecasting the UK housing market than the US market. There is convincing research that housing supply in the UK is inelastic (see Subsection 3.3), which suggests cyclical demand considerations could have a significant impact on prices.
Examples of government forecasters using the private sector average include the OBR and HM Treasury ( HMT), who, until December 2013, used an average of private sector forecasts for their 2-year ahead outlook for house price inflation (Auterson, 2014). Eighteen of the 38 external forecasters in HMT's October 2016 survey provided forecasts for housing price inflation for the UK as a whole for at least five quarters. [9]
Canada's federal Department of Finance uses the average of private sector forecasts for all key macro variables including real GDP growth, GDP inflation, real interest rates, and exchange rates. However, they use an internal macroeconometric model constrained to the consensus growth rates to decompose GDP into its components and income shares for fiscal forecasting, including housing prices and transactions. They have maintained the internal capacity for complete macro forecasting, but impose the private sector average as a basis for fiscal planning to "introduce an element of independence into the Government's fiscal forecast." [10]
Application (policy): fair. Neither of the three broad technical assumptions lend themselves to policy costings. However, there may be some scope to adjust assumptions to produce sensitivity tables and assess alternative assumptions-for example, if the growth rate of GDP or the consensus forecast of house price inflation were used, the rates could be adjusted by one percentage point and the consequences to the fiscal outlook could be reported. Alternative capacity for policy costings would need to be developed.
Accuracy (short run): fair. Forecasting by a technical assumption does not necessary mean sacrificing forecasting performance. On the strength of academic research on the unpredictability of many economic time series, practitioners are increasingly foregoing sophisticated forecasting techniques in favour of simple assumptions. For example, recent research such as Alquist and Vigfusson (2013) found that the common approach to forecasting the price of oil using the oil market futures curve cannot beat a simple no-change assumption. Their work has led many practitioners to abandon sophisticated oil price models. [11]
However, for the housing market, there is sufficient research to reject the idea that sophisticated models cannot improve upon technical assumptions. Researchers as early as Case and Shiller (1988) convincingly demonstrated that housing markets are not efficient (that is, they do not follow a random walk and observant investors can earn returns above a safe rate). This suggests housing time series are predictable. For example, if they experience one year of above-average growth, the next year tends also to be above average. Therefore, simple rules are unlikely to do well in cross-model comparisons based on accuracy.
Moro and Nuño (2012) tested their growth accounting framework empirically over the 1980s to late 2007 in four countries: the UK, US, Spain, and Germany. They found that it provides a useful description of housing price movements only in the US.
There is considerable evidence that averaging forecasts, as in the consensus approach, can provide superior forecasting performance (for example, Meulen et al. (2011) and Granziera, Luu, and St-Amant (2013)). However, in the case of many economic and fiscal variables, governments may have more timely and accurate information than private sector forecasters (for example, real-time VAT receipts). Private sector economic forecasters may also have biases unique to their circumstances. For example, there may be a bias in the public forecasts of private sector investment banks as a result of financial incentives (few would be enthusiastic to invest if the economic outlook is grim) and for mechanical reasons related to lags in recognising downturns (Batchelor, 2007).
Accuracy (medium run): fair. The medium run should benefit from forecast averaging or simple anchors based on high-level economic trends or the variable's history. However, there is some evidence that suggests otherwise. Tsolacos (2006) evaluates a consensus forecast of real estate rents (a returns index) and finds that while the consensus forecast for rents is best at a one-year forward horizon, simple time series approaches and regression models with interest rates outperform the consensus forecast two years out.
Communication (story telling): fair. Technical assumptions vary in their ability to tell a story-for example, using the historical mean or average growth rate would not reflect economic fundamentals, but growing prices or transactions with GDP may capture general economic trends. Growth accounting models allow broad trends to be discussed, but may not be able to explain short-run changes related to the business cycle.
The private sector average can tell a story fitting both overall economic trends and trends in the housing market, depending on how detailed the survey is; however, budget-to-budget revisions may be impossible to explain.
Communication (transparency): good. Presenting and explaining technical assumptions is relatively straightforward. All three approaches can be made independent and transparent. If the consensus forecast is viewed as a form of externally-imposed rule, it is transparent. However, the underlying methodology and assumptions that non-government forecasters use to produce the forecast would typically not be available.
Data compatibility: fair. Generally, technical assumptions have few data requirements, and the ones that do (such as for growth accounting models) are at a high level that will be available to Scottish forecasters. However, there are some limitations that reduce this score to fair.
First, using a private sector average may prove challenging for a forecast of the Scottish market. Relatively few institutions produce Scottish forecasts, and even fewer offer detailed forecasts down to the residential housing sector level, especially for a five-year forecast horizon. However, there are surveys of professional housing forecasters that may satisfy the requirements. [12]
The OBR suggests that although the consensus forecast was effective for communicating with stakeholders, it was abandoned largely because the data was not timely and definitions were problematic. This is summarised by Auterson (2014):
[the consensus forecast] had the advantage of being simple and transparent, but the disadvantage that there can be a significant lag between new information becoming available and external forecasts being updated, collated and published. This problem is particularly apparent when house price inflation is changing rapidly. Another drawback was that external forecasts reference a number of different house price indexes, meaning only a subset are directly relevant to the ONS house price series we forecast. (p. 1)
Finally, rules of thumb that rely on basic statistics such as historical means do not work well with trending data, seasonality, or level shifts (Makridakis, Wheelwright, and Hyndman, 2008). This will largely rule out these approaches for Scottish data in levels, but may be suitable for transformed data. This will require further evaluation.
Resources: good . Technical assumptions are cost effective and require few analytical resources and little to no specialist skills to apply. However, internal modelling capacity may still be required for policy analysis. Technical assumptions are easily estimated or imposed in spreadsheets and statistics software packages.
Our assessment of forecasting by technical assumption is summarised in Appendix Table A1.
3.2 Univariate time series approaches
Univariate time series models predict housing prices and transactions based solely on their own statistical properties, particularly the relationships of the variable with its values in the past (that is, the correlations and partial correlations estimated by regressing the variable on time-lagged values of itself). For example, if residential prices rose more quickly this year than their trend, it may be likely that they will also rise more quickly next year. These properties can be used to predict future values of prices and transactions without considering the wider economy. [13]
We look at three univariate forecasting approaches. First, the tendency for price or transaction shocks to dampen or persist can be modelled using a generalised approach called ARIMA modelling. Second, the behaviour of a series may change over different periods, such as when it is trending up or down (for example, during a housing boom or bust). This type of behaviour can be modelled using regime-switching methods. Third, univariate models can predict another property of the series: its volatility. This can be modelled using a GARCH process and may be useful in forecasting the risk to the budget outlook.
ARIMA
The general form of a univariate time series model is the autoregressive integrated moving average ( ARIMA) model, attributed to Box and Jenkins (1976), who first described the technique in detail and created a systematic approach for its estimation. [14]
ARIMA modelling attempts to capture two basic types of time series behaviour and their combination:
1. Autoregression
2. Moving average
The autoregressive ( AR) component presumes that housing prices or transactions are a function of lagged values of themselves. That is, future values can be forecast with current and past values by estimating the correlation of the series' value in time t with its values in time t-1, t-2, t-3, etc. The autoregressive model has the following general form (as given by Enders (2014)):
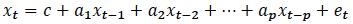
where c is a constant (often not required), e t is a random shock with constant variance, and p is the last lagged value that affects the current realisation.
The moving average ( MA) component presumes that housing prices or transactions are a function of random surprises in previous years - that is, the difference, or errors, between the model and actual observations as time advances.
The general form of an MA process is:
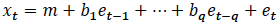
The MA in an ARIMA process is a different concept than the moving average smoothing techniques discussed in Subsection 3.1. Here it is a behaviour of the error term of the model-a similar averaging process, but applied to the forecast errors of the series, instead of its past values.
AR and MA models can be combined in a general univariate time series model-the ARMA model. A simple ARMA model that depends only on its value and error in the previous round takes the form:
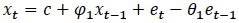
An ARMA model can be used only if the series is stationary, a condition unlikely to be met by housing market variables (an overview of Scottish housing market data along with a definition of stationarity is given in Box 2). For example, prices are likely to increase each year to some extent along with other prices in the economy (general price inflation). In this case, the mean (average) of house prices would grow over time. An ARMA process on the level of house prices would generally under-predict prices. But the series can be transformed to be stationary. If the trend is steady and predictable (in the inflation example, prices may follow the Bank of England's inflation target), the variable can be made stationary by detrending the data (regressing the series on a time trend). If, however, the data has a stochastic trend (that is, it is unpredictable), the variable must be transformed by differencing. [15] The latter case means the variable is integrated, which is the abbreviated letter I in ARIMA. [16]
Regime-switching models
Regime-switching models allow parameters to take different values in each of a fixed number of historical intervals. A change in the model's parameters may arise from a range of causes, such as changes to monetary policy or changes to the exchange rate regime (Stock, 2002).
Regime-switching models fall into two categories: threshold models and Markov switching models. In threshold models, regime changes arise from the behaviour of an observed variable relative to some threshold value. These models were first introduced by Tong (1983). They are formulated in general terms in Stock (2002) as:
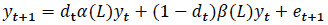
Where α (L) and β (L) create coefficients and lags of the variable against which they are multiplied, and d t is a non-linear function of past data that switches between the parameter regimes α (L) and β (L). Different functional forms of d t determine how the model transitions between regimes.
In Markov-switching models, the regime change arises from the outcome of an exogenous, unobserved, discrete random variable assumed to follow a Markov process (that is, the history of the variable does not offer any more information about its future than its current value). [17] The general form of a Markov-switching model is similar to the threshold model but the function d t represents the unobserved Markov process variable.
Forecasting volatility
The variance of an economic series is a measure of risk. If forecasters are interested in forecasting the risk to the LBTT outlook, or quantifying the variance of housing prices or transactions at different points in time, the series' own history can be used to forecast the variance. This is known as generalised autoregressive conditional heteroskedastic ( GARCH) modelling, where heteroskedastic means that the variable's volatility is not constant over time.
GARCH models were developed first by Engle (1982) and later refined by Bollerslev (1986). GARCH may be thought of as an extension of the ARIMA method that forecasts using the typical time series behaviour of both the values of a series, and its variance.
The following equation is a simplified GARCH model, based on Enders (2014):
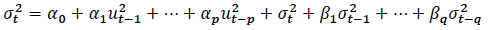
where u is the error term of a simple AR(p) process and 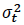 is the conditional variance of u which depends on the information available at time t-1.
is the conditional variance of u which depends on the information available at time t-1.
Box 2: Overview of Scottish residential prices and transactions
Figure B1: Scottish residential housing prices and transactions
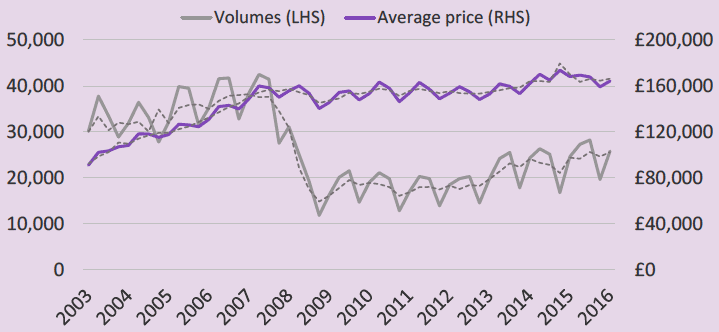
Figure B1 plots Scottish housing prices and transactions volumes from the Registers of Scotland, along with the seasonally adjusted series using the X-13 ARIMA- SEATS procedure of the US Census Bureau.
Housing prices and transactions contain a trend and seasonal pattern. Both series were affected by (and in turn affected) the downturn following the global financial crisis. Between late 2007 and early 2009 housing transactions collapsed to around a third of their pre-crisis levels. The fall in transactions coincides with a structural break in trend prices, ending the strong growth preceding the crisis.
A main concern when specifying a forecasting model is whether a series is stationary-that is, it has a constant mean and variance over time. Both smoothed series show a clear trend over time and transactions seasonality seems to widen after 2013. This suggests the data is non-stationary (and indeed housing market data in the UK and abroad is routinely found to be non-stationary (see Barari et al. (2014), among others). To use many of the forecasting techniques evaluated in our review, the data would need to be transformed, either by deseasonalising if they are found to be stationary in level terms (for example, through using dummy variables to capture seasonality), detrending if they are found to be stationary around a constant time trend, or differencing if they are found to be stationary around a stochastic trend (this can include seasonal differencing, that is, using the annual growth rate for each quarter). Alternatively, special techniques can be used to maintain the model in levels (see Subsection 3.5 - error-correction models).
Modelling is further complicated by policy changes such as the stamp duty holiday between September 2008 and December 2009, the introduction of graduated "slice" tax rates (similar to how personal income taxes are structured) to replace the previous "slab" rates on 4 December 2014, and the transition from the reserved stamp duty land tax ( SDLT) to the devolved land and buildings transaction tax ( LBTT) on 1 April 2015.
Assessment
Application (forecasting): good. ARIMA, regime-switching, and GARCH models have been applied to forecasting housing prices and transactions in a wide range of academic literature.
Potentially useful applications of ARIMA models to prices include Barari, Sarkar, and Kundu (2014), Stevenson and Young (2007), and Crawford and Fratantoni (2003), among others. For applications to volumes measures for transactions and housing supply, see Fullerton, Laaksonen, and West (2001).
Among practitioners, ARIMA modelling was the approach used by the Scottish Government in Draft Budget 2016-17 for forecasting average house prices in the first two year of the outlook, and for the whole five-year forecast horizon in Draft Budget 2017-18. Outside of Scotland, it is not widespread, but is often used as a benchmark comparison. ARIMAs are, however, used widely for economic forecasting and for revenues that are a small percentage of the overall tax take, or that do not have a tax base that lends itself to modelling directly.
Although we heard of no regime-switching models applied among practitioners, they are popular in academic research. For example, Park and Hong (2012 ) observed that monthly indexes of the US housing market are released at the end of the subsequent month. This, in turn, creates a month-long standstill in making judgements about the housing market. They exploit this interval to show how Markov-switching models can be used to promptly forecast the prospects of the US housing market within the standstill period.
Enders (2014) suggests that GARCH models are particularly suited to asset markets such as the housing market, as prices should be negatively related to their volatility (if market participants are risk-averse). Further, referring again to Box 2, it seems that the variance of house transactions in Scotland changes over time. The housing forecast may therefore benefit from GARCH modelling
Univariate models can produce ex ante forecasts without needing to be conditioned on auxiliary forecasts of exogenous variables (that is, they can forecast using only historical information available at the time of the forecast).
Application (policy): poor. All three methods of univariate forecasting are ill-suited for scenario analysis and fiscal impact costing, as they are not specified with explanatory variables to assess the impact of different economic assumptions and risk scenarios on the housing market. [18] ARIMA and GARCH models may have some limited use in risk assessments: ARIMA models can assess how exogenous shocks in one period are transmitted to future house prices and transactions in the future, and GARCH models may be able to improve upon estimates of annual revenue at risk.
Although of limited use for policy analysis themselves, univariate models may be a useful component of a broader policy analysis approach, such as for projecting components of the price distribution for the application of tax rates.
Accuracy (short run): good. ARIMA models showed mixed but broadly positive performance in out-of-sample forecasts, and in many cases, outperformed the more sophisticated models they were compared against. However, researchers are generally quick to assert that performance is dictated by the specific regions and time periods under study.
For example, the ability of ARIMA models to forecast Irish housing prices was evaluated by Stevenson and Young (2007) for the period 1998 to 2001. They found that ARIMA models provided more accurate forecasts compared to two other models-a multivariate regression and VAR model-on five forecasting accuracy measures: mean error, mean absolute error, mean squared percentage error, and error variance.
Lis (2013) estimated ARIMA models and other classes for rolling forecasts of the Canadian real estate markets in Vancouver and Toronto. Lis found that no single forecasting model performed best in all situations, but rather concludes that a forecasting approach should be chosen using detailed diagnostics for each series and time under study.
Brown et al. (1997) compared the ability of a regime-switching to predict house prices in the UK in the 1980s and 1990s to an error-correction model, an AR and a VAR model. They found that the regime-switching model performed the best in out-of-sample forecasts.
Meulen et al. (2011) constructed a unique price index using online real estate listings to control for different housing characteristics. They estimated a simple autoregressive model, as well as a VAR that incorporated information about macroeconomic trends. They found that the macroeconomic variables only slightly reduced the forecast errors compared to the naïve autoregression.
Maitland-Smith and Brooks (1999) found that Markov switching models are adept at capturing the non-stationary characteristics of value indexes of commercial real estate in the US and UK. The researchers found that it provided a better description of the data than models that allowed for only one regime (for example, a simple AR model).
Barari et al. (2014) estimated an ARIMA model and two regime-switching models on a 10-city composite S&P/Case-Shiller aggregate price index they created for seasonally-adjusted monthly data from January 1995 to December 2010. They found that the ARIMA model performs as well as the regime-switching models in out-of-sample forecasts.
Accuracy (medium run): fair. Forecast tests for univariate models in the academic literature are rarely performed more than two years into the future. The length of the useful forecast horizon is determined by the speed of decay, which is rarely significant beyond 8 quarters; however, when specified to decay to a simple trend, they may prove sufficient for the medium run.
Larson (2011) provides useful benchmark comparisons between univariate and multivariate models for three years into the future, finding that for Californian housing prices univariate time series models were outperformed by multivariate over the 1970s to late 2000s.
Communication (story telling): poor. Univariate time series models do not generally offer a direct causal interpretation of coefficients and can be difficult to communicate. That is, they predict what will happen, not why (Hyndman and Athanasopoulos, 2012). However, a univariate equation need not be entirely atheoretical, as a complex system of multivariate explanatory equations can often be transformed into a univariate reduced-form equation (Enders, 2014). In that manner, a univariate time series estimated by Ordinary Least Squares ( OLS) can capture the theoretical relationships of a wide assortment of underlying economic relationships. Nonetheless, the signs and magnitudes lose much of their ability to be interpreted, and the structural properties are impossible to recover from the final estimated equation.
Communication (transparency): fair. Equations and estimated coefficients would need to be published frequently, as specifications and estimates are likely to change with each addition of new or revised data. Fiscal sensitivity tables could not be estimated and published to provide a check on model revisions given economic developments. However, their relative simplicity lends them some merit, as scrutinizers with a general economics background would largely be able to understand and test the assumptions.
Data compatibility: good. The key advantage of this method is that it does not place a large burden on data collection-only historical data for the variable being modelled is required. Newton (1988) recommends a minimum of 50 observations for ARIMA modelling, which is in-line with the given history of reliable and detailed Scottish data. Univariate time series models are therefore well-suited to the available data for the Scottish housing market.
Resources: good. ARIMA models are an accessible forecasting model for small teams with limited technical background. Most software packages and forecasting guides have detailed procedures for the Box-Jenkins methodology that can guide the model selection procedure.
Our assessment of univariate time series models is summarised in Appendix Table A2.
3.3 Multivariate regression models
Rather than rely only on the past statistical behaviour of housing prices and transactions, forecasters can look for other factors that influence the housing market, such as interest rates and population. Models that include other explanatory variables are known as multivariate regression models. [19]
These models often use simple regression techniques such as OLS to predict future values of prices and transactions. They are similar to cross-sectional econometric analysis, except that explanatory variables are a function of time, and the estimated parameters can vary over time. For example, a simple multivariate forecast of housing prices may take the form: [20]
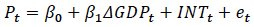
where: ΔG DP t = the change in gross domestic product, representing general sentiment about the strength of property markets and the wider economy.
INT t = some measure of interest rates, capturing the cost of borrowing, the discount rate on future housing benefits, and the risk-free rates on capital gains for competing investments, among others.
The variables to include and the model specification are guided by economic theory, particularly the interaction of demand for housing by households and the supply of housing by land and building developers.
Importantly, forecasting with multivariate models requires forecasts of the future values of explanatory variables that will need to be provided by exogenous forecast models ( Subsection 3.4 considers a technique where the future values of explanatory variables can be endogenously forecast).
Economic theories of the housing market
Multivariate regression equations in academic literature and practitioner research was most often based on asset-pricing theory. This approach was presented in an influential 1984 paper by Poterba. Asset-pricing models base the level of housing prices on an equilibrium concept with the 'income' that houses generate. [21] This income includes the value of housing services to the owner-occupier.
In Poterba's words:
A rational home buyer should equate the price of a house with the present discounted value of its future service stream. The value of future services, however, will depend upon the evolution of the housing stock, since the marginal value of a unit of housing services declines as the housing stock expands. The immediate change in house prices depends upon the entire expected future path of construction activity. The assumption that the buyers and sellers of houses possess perfect foresight ties the economy to this stable transition path and makes it possible to calculate the short-run change in house prices which results from a user cost shock. (1984, p. 730)
From another perspective, these models assume an arbitrage opportunity between buying and renting: if the cost of renting a house is lower than the expected cost of buying and occupying an equivalent house (the user cost of housing), then owners will sell and rent instead, increasing the supply of homes for sale and reducing vacant rentals until rents and user costs converge. A simplified specification of the user cost of housing could look like the following, based on Auterson (2014) and others:

where P t = the real price
i t = the net mortgage rate
τ t = the property tax rate
δ t = depreciation
m t = maintenance and repair expense
g t = expected capital gain (inflation plus the real expected price increase)
The market clearing rental rate is taken as a function of housing supply, or other variables such as real incomes and demographics.
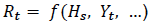
By setting the rental rate equal to the user cost equation and manipulating the resulting equation, growth in housing prices can be specified as an inverted demand function: [22]
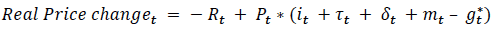
where g* is now the real expected capital gain. Auterson provides a description of how this model may be implemented in practice in the UK, including detailed data sources.
Implementing multivariate models in a forecast can involve simple applications of linear regression analysis with single equation specifications, for example an equation with price on the left-hand side (dependent variable). Models could also describe the housing market more generally with several equations, having price and transactions simultaneously determined, each driving one another within a feedback loop. The latter could include both structural and reduced-form systems of equations. [23]
Multivariate models could also be constructed using a bottom-up or top-down approach. In the bottom-up approach, relationships are estimated by looking at the factors that influence a house's value (such as the number of bedrooms, detached versus higher-density units) or real estate markets in different cities, and then aggregating to the national level based on population weights and construction trends. Models could also be applied separately for land and structures or for new construction versus existing turnover. Typically, however, structural relationships are examined at the top-down level. In a top-down approach, the relationship is examined at the national (aggregate) level using a model that relates aggregate average house price growth to macroeconomic variables such as growth in real incomes and employment.
Assessment
Application (forecasting): fair. There are many examples of multivariate regression models applied to forecasting housing prices and transactions in the UK and abroad. For example, Dicks (1990) extended the multiple equation demand and supply models of earlier researchers in the US to the UK market to forecast house prices for new and second-hand dwellings, as well as housing completions and the uncompleted stock of dwellings.
There is also a strong base of multivariate model research for the US market, owing to the richness and ease of access to data. In an influential paper, Case and Shiller (1990) pooled data across four US cities using OLS regression to examine how prices evolved based on explanatory variables such as the change in per capita real income, employment expansion, the change in the adult population, and changes in housing construction costs. [24] They estimate several specifications of forecasting models that prove to have significant forecast accuracy.
This approach is also common among practitioners. For example, the OBR's model as presented in Auterson (2014) describes the multivariate model they use to forecast the housing base for Stamp Duty Land Tax and for constraining the housing sector of the macroeconomic model. They model rental prices using real incomes, housing starts, and demographics, modifying the equation above to include an estimate of credit conditions, mrat, as follows: [25]
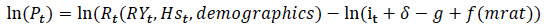
The OBR's model is based on several papers by Meen (2013, 2009, and 1990, among others) who has undertaken a wide range of research on the UK housing market.
Multivariate models of the housing economy can be used as auxiliary models outside of the main macroeconomic forecasting model, and their outputs can be imposed on the macroeconomy model, or, where accounting concepts are different or aggregated accounting identities need to hold, are used to apply judgement to the central model's equations (for example, see Kapetanios, Labhard, and Price, 2008).
Because multivariate models are conditioned on exogenous explanatory variables, they cannot produce ex ante forecasts. This reduces their score compared to models that can produce ex ante forecasts.
Application (policy): good. Multivariate econometric models are particularly relevant for policy assessments and fiscal impact costings. They can include a wide range of variables representing government policy and other explanatory variables that can be changed to estimate the cost of policy or to evaluate alternative assumptions. Makriditis et al. (2008) suggests governments have "few alternatives other than econometric models if they wish to know the results of changes in tax policies on the economy (p. 301)."
Accuracy (short run): fair. Single equation models can be tailored to fit the historical data perfectly, if enough explanatory variables are added. This is not necessarily an indication of useful forecasting performance, however, and in fact can lead to the opposite-overfitting and poor out-of-sample forecasts.
Dicks (1990) discussed the overfitting issue while estimating a number of simple demand and supply equations for the UK market based on earlier research by Hendry (1984). Dicks found that extending the demand and supply models to include the mortgage market, demographic factors, and construction costs can improve short-run forecasting results for prices and volumes and achieved reasonable results for the 1970s and 1980s, albeit with a tendency to under-predict the rate of house price increases.
Forecasting with a regression model requires conditioning the model on future values of explanatory variables. Other models will need to provide these variables, such as household income from a macroeconomic model. The forecast accuracy will be largely determined by these exogenous forecasts.
Accuracy (medium run): fair. Although forecasts using explanatory variables introduce an additional source of uncertainty, anchoring the medium run forecast to fundamentals may nonetheless provide an improvement over naïve forecasts (Lawson (2011) confirms this for the case of Californian housing prices and provides a discussion). However, as most relationships must be specified in terms of their growth rates to achieve stationary data, the medium-run performance is likely to perform poorer than other models that permit long-run levels relationships (see Subsection 3.5).
Communication (story telling): good. Multivariate regression models must be conditioned on future values of exogenous explanatory variables. This makes them well-suited for story telling and integration within a wider budgetary framework to provide a consistent budget narrative.
Communication (transparency): good. They can provide a clear explanation for forecast errors. Equations can be published and their specification (particularly model coefficients) is unlikely to change frequently. Further, model coefficients have intuitive interpretations that can be easily evaluated and repeated by budget scrutinisers with a general background in economics.
Data compatibility: fair. Multivariate regression models work well with the number of observations of quarterly data available for the Scottish housing market. The data required for the asset-price approach appears to be available, including housing starts and completions, although there may be limitations on the length of rental series. There is also sufficient data for affordability models, including interest and total payment to income ratios available from the Council of Mortgage lenders. That said, there are likely to be some restrictions on the set of explanatory variables for Scotland, rather than the UK as a whole, and the data requirements are more involved than univariate models, resulting in a fair score.
Resources: fair. Econometric models are not push-button and require more resources than purely statistical models such as in Subsection 3.2. They require fewer resources than other techniques in the review such as DSGE models, but nonetheless require specialised knowledge about both housing markets and econometric theory. They require frequent maintenance, re-estimation, and re-specification. Makridakis et al. (2008) provide a useful discussion of the resources devoted to econometric models versus simpler univariate approaches:
Whether intended for policy or forecasting purposes, econometric models are considerably more difficult to develop and estimate than using alternative statistical methods. The difficulties are of two types:
1. Technical aspects, involved in specifying the equations and estimating their parameters, and
2. Cost considerations, related to the amount of data needed and the computing and human resources required. (p. 302)
On the question of whether the extra burden of multivariate models over univariate approaches is justified, Makridakis et al. provide an opinion based on their own experiences, that suggests the appropriateness of a multivariate econometric model will ultimately depend on its intended use within the Scottish Government's budget production framework:
The answer is yes, if the user is a government, maybe if it is a large organization interested in policy considerations, and probably not if it is a medium or small organization, or if the econometric model is intended for forecasting purposes only. (p. 302)
Our assessment of multivariate models is summarised in Appendix Table A3.
3.4 Vector autoregressive models
The basic vector autoregressive model ( VAR) is a collection of time series models for different variables, estimated at the same time as a system. VAR models offer a simple and flexible alternative to the multivariate regression models of Subsection 3.3. The VAR approach need not rely on economic theory to specify relationships between variables (though theory often drives the choice of variables to include). VARs are instead based on the idea that economic variables tend to move together over time and tend to be autocorrelated.
Sargent and Sims (1977) promoted VARs as an alternative to large-scale macro-econometric models. They criticised macro models for the strong assumptions they imposed on the dynamic relation between macroeconomic variables and for not accounting for the forward-looking behaviour of economic agents. [26] They proposed an alternative that allows the data itself to determine how macroeconomic aggregates interact.
In VAR equations, the time path of the variable of interest can be affected by its past values and current and past values of other variables, while also letting the other variables be affected by current and past realizations of the variable of interest and each other-that is, they allow feedback between variables. [27] For a simple case of two variables, it has the following form, taken from Enders (2014):
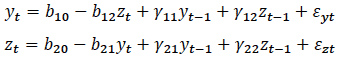
While the VAR model does not need to make any assumptions (impose restrictions) about which variables affects the other, an economic theory-based model can be imposed on a VAR, along with other behavioural and reduced-form (no contemporaneous effects) specifications.
If some series are thought to be determined exogenously or the researcher is working with ragged edge data (releases of some series are available before others) their values can be imposed exogenously. An example may be the outlook for the policy rate path of the Bank of England. However, Brooks and Tsolacos (2010) note that comparisons between unconditional and conditional VARs find little improvement in forecast accuracy from using conditioned exogenous variables. VARs can also include exogenous variables such as time trends, seasonal dummies, and other explanatory variables. Non-stationary data (as is likely to be the case for Scottish prices and transactions) may need to be transformed (using logged differences or growth rates) before entering the VAR.
Assessment
Application (forecasting): good. VARs are well-designed for forecasting and are commonly used across a wide range of forecasting applications in the public and private sector. Because they contain only lags of variables, future values can be forecast without forecasting other determinants in separate models and imposing them exogenously or assuming their time path-that is, they are not conditioned on any future realisations of explanatory variables.
Brooks and Tsolacos (1999) provide a useful example of a VAR applied to the UK housing market. They estimated the impact of macroeconomic and financial variables on the UK property market, as measured by a real estate return index. They chose monthly data to be comparable to US studies over the period December 1985 to January 1999. The variables were selected based on other non- UK studies that have determined the variables' relevancy under various theoretical and empirical specifications. The variables include: the rate of unemployment as a proxy for the real economy (as its available at the monthly frequency), nominal interest rates, and the spread between long- and short-run rates, unanticipated inflation, and the dividend yield. They find that macroeconomic factors offer little explanatory power for the UK real estate market, although the interest rate term structure and unexpected inflation have a small contemporary effect.
Even if not used as the main forecast, VARs frequently serve as a yardstick against which to measure the forecasting performance of other more resource-intensive models, such as large-scale macroeconometric models.
Application (policy): poor. It is generally difficult or impossible to recover interpretable directional causal relationships from a VAR in practice. VARs are therefore not useful for scenario analysis or fiscal impact costings. Certain structural forms of VAR models have some use for performing risk assessments, for example, the impulse response of a real income shock on housing prices.
Accuracy (short run): good. VARs are often found to perform better than univariate time series and more complex theory-based models. They are especially suited for the short-run horizon. This is conditional on having sufficient Scottish historical data that doesn't limit the VAR's specification.
Accuracy (medium run): fair. Because VARs specifications are not grounded in long-run causal relationships based on theory, forecasts for the medium-term may suffer. There were generally few applications of VARs beyond 8 quarters.
Communication (story telling): poor. By not imposing a strict theoretical structure, VARs allow the data to drive the forecast. Although this makes for a better forecast, it makes interpretation difficult. The complex lag structure (and contemporaneous impacts of variables if so specified) makes it difficult or impossible to isolate the influences of variables on each other to tell a story.
A VAR may have trouble being made consistent with other budget forecasts and the economic narrative, depending on the specification. Under certain conditions it can be constrained to other forecasts or conditioned on exogenous variables from the economic model or other fiscal variables.
Communication (transparency): fair. VAR specifications are likely to change frequently and would need to be published frequently. External budget scrutiny and testing of equations would be limited to specialists. However, the limited judgment involved with running a VAR model adds to its transparency.
Data compatibility: fair. Because of the lag structure in VARs, adding additional variables increases the number of parameters that the number of parameters to estimate dramatically. More parameters require more observations. To conserve degrees of freedom, standard VARs are generally quite small, with around six to eight variables (Bernanke, Boivin, and Eliasz, 2005). Given the relative limitations of Scottish data compared to UK and US data, this is likely to be even fewer. Although the number can be expanded with Bayesian techniques (see Section 4), in practice it may be necessary to discard potentially useful variables simply to estimate the model. A problem may emerge for Scotland if there are sufficient observations to estimate the VAR, but not enough to include enough lags to whiten residuals. This issue can be surmounted by common factors analysis laid out by Bernanke et al. (2005), Stock and Watson (2002) and discussed further in Section 4.
Resources: good. VARs can be implemented quickly and largely programmatically in statistics software packages, using automatic criteria for selecting the model's lag length. They are unlikely to require significant resources or specialists.
Our assessment of VARs is summarised in Appendix Table A4.
3.5 Error-correction models
The forecasting techniques discussed so far can be used only if house prices, volumes, and explanatory variables are stationary or transformed to be stationary-that is, their means and variances are constant over time. [28] House prices and transactions in Scotland and elsewhere tend to grow over time. Further, their quarterly fluctuations (variance) tend to be different during different periods.
Differencing the series to apply ARIMA and VAR approaches allows model coefficients to be estimated with OLS regression, but may sacrifice explanatory power between variables in their levels form. Further, there would no longer be a long-run solution to the model. In economics applications, this long-run solution means that the system is in equilibrium and there are no longer short-run fluctuations. [29] This would be the case, for example, in situations where the output gap is closed and economic variables have returned to their long-run steady state (such as in the outer years of a five-year budget forecast). For the housing market, this long-run solution is generally considered as the horizon over which supply is elastic.
Error-correction models were developed to overcome the limitations of differencing to preserve the long-run levels information and present both the short-run growth information and the long-run equilibrium relation in a single statistical model. This makes them particularly powerful for forecasting the real estate market, given that it has been shown that this long-run information contains useful information (as discussed above in Subsection 3.3).
Error-correction mechanisms are based on the concept of cointegration: two or more non-stationary variables may wander around, but will never be too far apart-that is, the gap between them is stable over time, and the gap is itself stationary.
This empirical connection is the result of a theoretical equilibrium market force or shared trend. Researchers applying error-correction models to the housing sector point to several such potential cointegrating relations:
- household incomes and house prices
- rental rates, the discount rate (interest rates) and house prices
- house prices, GDP and total employment
A basic error-correction model is represented by the following equation, based on the presentation in Enders (2014):
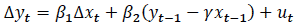
The two difference terms (differencing is represented by Δ) are stationary. The term 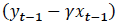 is an algebraic manipulation of the long-run levels model, and it represents that amount by which the two variables were out of equilibrium the period before (that is, the error). For example, this could be the amount by which imputed rents from owner-occupied homes are out of sync with quality-adjusted actual rents. Because
is an algebraic manipulation of the long-run levels model, and it represents that amount by which the two variables were out of equilibrium the period before (that is, the error). For example, this could be the amount by which imputed rents from owner-occupied homes are out of sync with quality-adjusted actual rents. Because 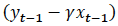 is stationary, the model can be estimated with OLS and statistical inference is valid. The coefficient β 2 is the speed at which the disequilibrium is corrected (for example, a coefficient of 0.5 would mean roughly half the gap between imputed rents and quality-adjusted actual rents is closed one period later.
is stationary, the model can be estimated with OLS and statistical inference is valid. The coefficient β 2 is the speed at which the disequilibrium is corrected (for example, a coefficient of 0.5 would mean roughly half the gap between imputed rents and quality-adjusted actual rents is closed one period later.
Error-correction models rely on the same theoretical underpinnings as the multivariate regression models in Subsection 3.3. Indeed, many of the specifications and models discussed in 3.3 are more appropriately implemented as error-correction models.
Assessment
Application (forecasting): good . There is a vast literature that applies error-correction models to the housing sector. An influential error-correction model framework for housing supply and prices was developed by Riddel (2000, 2004). It allows both disequilibrium in housing supply and house prices to affect one another. Stevenson and Young (2014) applied the model to the Irish housing market, which may serve as a useful guide for modelling the Scottish market. In this model, the long-run supply equilibrium is estimated empirically by the equation
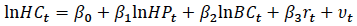
and the error-correction specification is
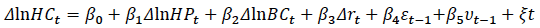
where: HC t = housing completions
HP t = prices
BC t = real building costs
r t = the real after tax interest rate
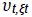 = error terms
= error terms
ε t-1 = the lagged disequilibrium (error) from the long-run price equation below
The long-run price equilibrium is an inverted demand function, estimated by the equation
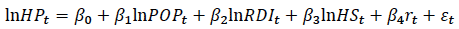
and the error-correction specification of the price equation is
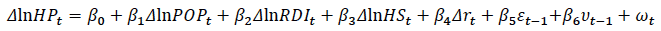
where: POP t = population aged 25 to 44
RDI t = real disposable income per capita
HS t = is the per capita housing stock
ω t = error term
Addison-Smyth, McQuinn, and O'Reilly (2008) modelled Irish housing supply using error-correction models and found that developers do respond to disequilibrium. However, the findings also suggest the gap is slow to correct itself, with only roughly 10 per cent of the disequilibrium being corrected annually.
Error-correction models are perhaps the most common way to model the housing market in finance ministries and central banks. For example, all three major public macro forecasters in the UK ( HMT, OBR, and the Bank of England) rely on error-correction models.
Application (policy): fair. Error-correction models rely strongly on economic theory and are relevant for policy analysis. They can include a wide range of variables representing government policy and other explanatory variables that can be changed to evaluate alternative assumptions. That said, their focus is on forecasting the dynamic impact of these variables, and they rely on cointegrating relationships between variables that may not exist between the policy levers of interest for fiscal impact costing, and so are less relevant to policy than multivariate regressions or microsimulation models with a fiscal impact costing focus.
Accuracy (short run): fair. Error-correction models generally perform well in both the short run and the medium run. However, there is some evidence that in the UK they may underperform in the first eight quarters of the outlook. The OBR has found that the error-correction model it uses to model the housing market ( HMT and the Bank of England use similar approaches) is not well-suited for capturing short-run dynamics, although it provides good forecasts in the medium run (Auterson, 2014).
Accuracy (medium run): good . Because of their basis in theory and being ground in long run levels equilibrium relationships, error correction models are likely to provide better forecasting performance over years three to five than other methods. Lawson (2011) found convincing evidence that error-correction models outperform a number of other univariate and multivariate models over a three-year horizon for Californian housing prices when estimated over the period 1975 to 2006 and forecast over 2007 to 2009. Larson also found that error-correction models could predict a housing price decline well in advance (the ability to forecast the timing of the decline, however, was poor).
Communication (story telling): good. Like multivariate regression models, error-correction models are conditioned on future values of exogenous explanatory variables. This makes them well-suited to story telling and integration within a wider budgetary framework to provide a consistent budget narrative.
Communication (transparency): fair. Equations can be published and their specification (particularly model coefficients) is unlikely to change frequently. Model equations are more opaque to budget scrutinizers with only a general economics background than more simple regression equations, but the equations are nonetheless more economically intuitive than VARs.
Data compatibility: fair. While it is possible to estimate an error-correction model using Scottish data, there may be some limits that could affect forecasting performance. Practitioners suggest that housing cycles modelled with error-correction models can last eight to ten years, and that these dynamics will form the basis for estimating the error-correction model's parameters. Suitable Scottish historical data may only capture one cycle, and that cycle included the financial crisis.
Resources: fair. Error-correction models are likely to require greater expertise to develop, run, and maintain, than many other options. However, the specification and forecasting can be done easily in statistical software packages by specialists, and is not likely to require significant time or effort following the initial development period.
Our assessment of error-correction models is summarised in Appendix Table A5.
3.6 Large-scale macroeconometric models
Forecasts of the housing market are produced within the macroeconomic models of budget forecasting frameworks to estimate the residential investment component of GDP, an important driver of business cycles.
Macroeconometric models simulate the economy as the interaction of aggregate supply and aggregate demand on the same basis as the National Accounts statistical framework. They use a mix of the techniques above to specify equations that describe the working of the entire economy. Although not employing new tools, the systems approach and the way it is implemented in practice-particularly national accounts data and identities and the goal of forecasting GDP-deserves special consideration as a model class on its own.
Macroeconometric models are loosely grounded in Keynes's General Theory, which Hicks (1939) and later researchers formulated into the well-known IS- LM framework. The estimation of a system of econometric equations estimated one equation at a time (ad hoc basis) related together using national accounting identities was first undertaken by Klein and Goldberger (1955) for the Cowles Commission (an initiative running from 1939 to 1955 to apply mathematical and statistical analysis to the economy). [30]
Models typically take a view of the output gap (the economy's actual output relative to its potential output, forecast separately) and combine it with other macroeconomic relationships such as the IS curve (aggregate demand and interest rates), Phillips curve (unemployment and inflation), a Taylor rule (monetary policy), and interest parity conditions (exchange rates). They strike a middle ground between theory-based and pure time-series models, taking aspects of both to capture both theoretical relationships and rich dynamics of variables over time for forecasting.
The housing sector (private sector investment in dwellings in the UK, often called residential investment or residential gross fixed capital formation elsewhere) includes purchases of new housing and major improvements to existing dwellings by households (Carnot et al, 2014). [31] It is an important determinant of (and is determined by) household wealth and consumption with the model framework. It is estimated using aggregate behavioural equations within the household sector to derive the wealth stocks of consumers that, along with disposable income, guide the household sector's consumption equations.
A typical equation for the real stock of housing resembles the following combination of a short run difference and long-run levels equation (error-correction model), from Carnot et al. (2014):
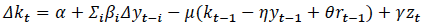
where: y = real disposable income
k = residential investment
r = the real interest rate (usually a long rate, but Carnot suggests a short rate in the UK, where mortgages are predominantly at variable rates)
z = other explanatory variables such as the relative price of housing
The justification for this specification is often grounded on the neo-classical standard model of life-cycle utility maximisation, where consumers choose between a mix of consumption goods and housing investment goods. This is, however, only a loose theoretical justification-it is not necessarily implemented by specifying a household utility function, which is the realm of DSGE models discussed in Subsection 3.8. The degree of foresight and optimisation of the household can differ. They can have perfect foresight (Robidoux and Wong, 1998) or include some rule of thumb consumers, to introduce an element of constrained rational expectations (Gervais and Gosselin, 2013).
Housing prices are usually modelled as a rental price for housing services (for owner-occupied homes this is the best estimate of what the owner would charge if she were renting it to herself). The price then feeds into the rate of return on housing investment, which drives investment in residential housing and affects future supply. [32]
Traditional macroeconomic models continue to be the workhorse of macro modelling in government departments and central banks. Although DSGE models were implemented in many central banks and finance ministries, they are general used for scenario analysis in parallel with macroeconometric models and to challenge the forecast from an alternative perspective. Further, traditional large-scale macroeconometric models are experiencing a resurgence in popularity and credibility (for example, see the academic and online discussions generated by Romer (2016)).
Assessment
Application (forecasting): fair. Finance ministries and central banks are moving toward making their macroeconometric model documentation public. There are many published examples that forecasters could use as a foundation on which to build the model using Quarterly National Accounts Scotland.
For example, the housing sector component of the macroeconometric model shared by HMT and OBR is described in OBR (2013). It forecasts private sector investment in dwellings ( RES t in £m and chained volume measures) using the following relationship with real house prices, the real interest rate, and the number of property transactions:
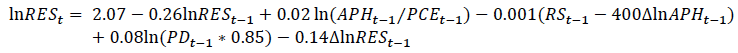
where: APH t = an average house price index
PCE t = the consumer expenditure deflator
RS t = UK three month inter-bank rate
PD t = property transactions
Property transactions (particulars delivered) are assumed to be negatively related to the difference between actual and expected house prices, where expected house prices are determined by the user cost of capital, consumer prices, and real disposable income, given by:
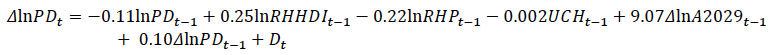
where: RHHDI t = real household disposable income
RHP t = real house prices, APH t / PCE t
UCH t = user cost of housing (a function of mortgage rates and the change in prices in the previous period as a proxy for the expected capital gain)
A2029 t = population of cohort aged 20-29
D t = a collection of dummy variables to control for abnormal events
The remaining equations of the model estimate the other components of aggregate demand: consumption (durables and current), investment, government spending, exports, and imports (see OBR (2013) for the complete specification).
There is a robust literature demonstrating the importance of the housing sector's role in the macroeconomy and importance of considering it within this wider framework
For example, the correlation between the growth in housing prices and the growth in consumption and savings has been demonstrated by Meen (2012), who estimated the correlation coefficient as 0.74 on average over 1982 to 2008. The relationship has broken down somewhat since the turn of the century, however. The correlation in the period 1982 to 1999 was 0.81 and for 2000 to 2008 was 0.65.
In the US, Case et al. (2005) provide a useful summary and theoretical framework, finding house wealth to be more important than other forms of financial wealth for driving consumption patterns.
Although the correlation between housing prices and consumption and saving behaviour is well established, conclusive evidence of causality has remained elusive. Elming and Erlmler (2016) reviewed the relevant literature and found four main links between house prices and consumption: 1) the housing wealth effect, 2) housing equity serving as collateral and precautionary wealth, 3) the common factor of income expectation, and 4) the common factor of overall credit conditions and financial liberalisation. The authors provide convincing evidence in favour of a direct causal influence of housing prices on consumption. They do so by exploiting the natural variation between household price drops in different regions during the global financial crisis, using households with two public service income earners to control for income expectations (the public service salaries are set through strict collective bargaining arrangements).
Macro models could form part of the overall budget and help inform the housing market forecast; however, their applicability to the LBTT forecast itself may be limited. Macro models typically use a different concept of average house prices than would be useful for the tax base, and would need to be modified to serve that purpose. Many institutions use an auxiliary model, which is estimated outside the forecasting framework and they impose the model results exogenously (Auterson, 2014).
The aggregate time series in the national accounts, such as residential investments, may have limited ability to predict house transactions. Mankiw and Weil (1989) discuss how the noise (large standard errors) of national accounts data obscures relationships that show up when estimated using other time series grounded in administration or census data.
Application (policy): fair. Macroeconometric models can be used for policy analysis. For example, HMT used the macro forecast and OBR's auxiliary housing market model to assess the impact of a vote in favour of leaving the EU on house prices ( HMT, 2016). They can be used to model economic and fiscal sensitivities to shocks such as an oil price decline, and prepare fiscal multiplier estimates (Office of the Parliamentary Budget Officer, 2016). However, they may be of limited use for fiscal impact costing, because of the differences between housing investment in the national accounts and the tax base.
Accuracy (short run): fair. Early macroeconomic models that were driven by theory alone, ignoring the dynamics and inter-temporal properties of the data, generally produced poor forecasts. [33]
Forecast performance has since been improved with the introduction of better techniques to capture dynamics, and modern macroeconometric models should fare relatively well for their purpose. Granziera and St-Amant (2013) compares the forecast of their rational ECM framework of the housing markets to AR and regular ECM models and finds it performs better both four quarters and eight quarters ahead in rolling forecast experiments over 2002 to 2011.
As discussed, macroeconometric models are a blunt tool for forecasting tax bases. Conforming to national accounting identities restricts the specification of the tax base (housing transactions can relate to non-current production). Correspondence between tax bases and national accounts aggregates can be poor. They tend to perform more poorly than a model dedicated to the specific tax base and tax program parameters.
Accuracy (medium run): fair. Because of their theoretical underpinnings, use of long-run equilibrium conditions (closing of the output gap), and a greater ability to maintain variables in a levels specification (making use of error correction models), these models are likely to improve upon naïve forecasts for the medium run. However, long-run macroeconometric forecasts suffer from the same concerns regarding tax base congruence as in the short run.
Communication (story telling): good. Large-scale macroeconometric models offer relatively straightforward, intuitive relationships that can be communicated easily. Parameter signs and magnitudes should make intuitive sense and align with economic theory. Because of their reduced-form specification, interactions between equations and simultaneously determined outcomes are limited relative to an unrestricted systems approach. Impulse response charts can be produced and published publicly to demonstrate the characteristics of the model.
Communication (transparency): fair. Model documentation, equations, and datasets can be published online for public scrutiny by interested parties such as academics, think tanks, and private consultancies (for example, the ITEM group at Ernst and Young uses HM Treasury's model for its own consultancy purposes, including an annual report that provides a check on the government's forecasts). [34] Parameter estimates and equation specifications should remain relatively stable between forecast. That said, the transition from history to model results involves a lot of smoothing and adjustments to fit with economic monitoring. The modeller's judgment plays a large role in the starting point, first two quarters, end point, and dynamics in between. For this reason the model only receives a fair score.
Data compatibility: fair. Estimating a large-scale macroeconometric model should be possible using the Scottish Quarterly National Accounts. However, drawbacks related to congruence with the tax base could be amplified as a result of Scottish data limitations, as there are only high-level sector accounts for residential gross fixed capital formation on an experimental basis.
Resources: poor. One or two experienced and skilled analysts are sufficient to maintain a large-scale macroeconometric model once developed; however, the development is a significant undertaking. Practitioners reported that it is useful to have several less-experienced analysts in charge of economic monitoring and to work independently on model components such as import/export modules. Model development would require programmable statistics software beyond Excel.
Our assessment of large-scale macroeconometric models is summarised in Appendix Table A6.
3.7 Dynamic stochastic general equilibrium models
Dynamic stochastic general equilibrium ( DSGE) models are a systems framework for modelling the aggregate economy. They are relied upon heavily in modern macroeconomics. There is a broad spectrum of models falling under the DSGE label and an exact definition is difficult to pin down. De Vroey (2016) suggests that early DSGE models were defined by the following elements, based on his interpretation of Manuelli and Sargent (1987):
- a general equilibrium perspective (markets are not considered in isolation, but rather as a whole)
- dynamic analysis (the decisions and behaviour of economic agents depend are modelled over time, rather than a single period)
- rational expectations (the forecasts of agents within the model are assumed to be the same as the forecasts of the model (see Sargent, 1987))
- microfoundations (economic agents are modelled with optimizing behaviour, for example utility-maximizing and forward-looking behaviour in household decisions on saving, consumption, and labour supply subject to a budget constraint)
- markets clear (prices adjust to eliminate excess demand or supply)
- exogenous stochastic shocks (shocks come from outside the system rather than emerging within)
These features, along with other elements such as production technologies, budget constraints, and decision rules are formulated mathematically to represent the economy in a manner that a computer can simulate and solve. Equations are estimated all at once in a binding, unified way rather than the piecemeal equation-by-equation method of traditional macroeconometric models (Carnot et al, 2011).
Although early models assumed macroeconomic fluctuations were the result of random disturbances in technology and preferences, they were eventually modified to be based on frictions (price and wage rigidities) and to include monetary policy, with these new classes of models being called New Keynesian models (for example, see Christiano, Eichenbaum, and Evans (2005)).
DSGE models emerged out of the real business cycle literature, notably Kydland and Prescott (1982). Slanicay (2014) provides a history, describing them as a response to the forecasting failure and problematic theoretical underpinning of large-scale macroeconometric models-namely, the simultaneous high inflation and high unemployment of the 1970s (a breakdown in the Keynesian Phillips curve) and lack of microfoundations.
A technical specification of the equations of DSGE modelling would go beyond what is possible in this review, but we provide a qualitative description of a small-scale new-Keynesian DSGE model, based loosely on An and Schorfheide (2007) as presented by Herbst and Schorfheide (2015).
The basic DSGE economy is modelled using five agents. There are two types of firms: a single representative final goods producing firm that is perfectly competitive, taking input prices and output prices as given. The firm's inputs are supplied by intermediate goods producing firms that are monopolistically competitive, choosing labour inputs and output prices to maximise the present value of future profits. Households choose their labour supply, consumption, and saving to maximise utility, subject to a budget constraint that accounts for investment returns and tax payments. A central bank uses an interest rate feedback rule to respond to monetary policy shocks and targets a steady-state inflation rate consistent with a level of output at its potential. A fiscal authority is assumed to consumes a fraction of aggregate output subject to a budget constraint and levies a lump-sum tax to finance any shortfalls in government revenues.
Examples of DSGE models that could be drawn upon for Scottish forecasting include the Bank of England's COMPASS, the Bank of Canada's ToTEM, and the New York Federal Reserve's FRBNY models. The IMF also uses two well-known DSGE models: MultiMod and GEM.
DSGE models have faced criticism following the financial crisis and their use and misuse is being keenly debated. Their opponents include Romer (2016), who criticises DSGE models broadly, attributing their popularity to "imaginary" constructs that succeeded through mutual loyalty among well-known economists and a departure from scientific principles.
A particular target of criticism is the model's rational expectations assumption, although methods to introduce frictions have been implemented to slow adjustments to reflect observed behaviour, and more recently models such as Slobodyan and Wouters (2012) have introduced bounded rationality.
Assessment
Application (forecasting): poor. The focus of DSGE models is not forecasting, but rather simulating and tracking how shocks are propagated through the economy. Slanicay (2014) describes their range of application, from the models that central banks use to discuss the transmission of monetary policy shocks through the economy, to the more stylised academic models tailored to test and demonstrate implications of particular economic assumptions.
Applications of DSGE models to the housing market are limited. Basic DSGE models typically only operate in flow space (changes period-to-period) and residential investment stocks generally do not play a role. That said, there have been some efforts in recent years to incorporate a housing sector.
For example, Caldara, Harrison, and Lipinska (2012) developed a method to use the correlations between housing price shocks estimated in auxiliary VAR models with variables included in the DSGE model to assess the implications of shocks to US housing market data.
Other research comes from Iacoviello and Neri (2010). The authors considered both the impact of macroeconomic shocks on the housing market and how shocks to the housing market affect the macroeconomy. The housing market is incorporated via a production function that produces houses using capital, labour, and land.
A recent innovation in DSGE models is the stock-flow consistent models of Burgess, Burrows, Godin, Kinsella, and Millard (2016). They show promising improvements on traditional DSGE models, incorporating the balance sheets of economic sectors including the housing sector. Stock-flow consistent DSGE models may be more suitable for housing market forecasting and policy in the future.
Application (policy): fair. DSGE models may have use for modelling the transmission through the economy of housing market scenarios. DSGE models are not appropriate for static fiscal impact costing (costings that are estimated using a single market and do not consider the feedback effects of the rest of the economy). However, they can be used for dynamic scoring (modelling and costing the feedback of government policy changes through the wider economy).
Accuracy (short run): fair. Although early DSGE models had poor forecasting performance, recent developments such as Smets and Wouters (2007) have demonstrated refinements that can offer better forecast properties. The fair score has been given for the general forecasting performance of DSGE models, but forecasters should consider that application to the housing market is largely untested.
Accuracy (medium run): fair. DSGE models may offer better performance in the medium run than other models less grounded in economic theory. Iacoviello and Neri (2010) find their housing-market augmented DSGE model is able to capture long-run trends and the medium-run business cycle well. When choosing a DSGE model for the medium-run horizon, there is evidence that smaller is better. For example, Del Negro and Schorfheide (2012) assess the forecast performance of the large-scale Smets and Wouters (2003) DSGE model against a small-scale version. They find that although the short-run forecast performance of the large-scale model is slightly better than the smaller model, the medium-term forecast performance of the compact model is superior.
Communication (story telling): fair. DSGE micro foundations lend themselves to intuitive narratives. However, complexity of interactions runs significant risks of becoming a 'black box' with difficult or no interpretation.
Communication (transparency): poor. Caldara et al. (2012) suggest that as layers of complexity and interaction are added, the results and interactions become more opaque and harder to explain to policymakers. Considerable judgment is applied throughout estimation. External scrutiny would require specialist training.
Data compatibility: good . A DSGE model could be estimated using the Quarterly National Accounts of Scotland. The Smets and Wouters (2007) model is constructed using only seven data series (real GDP, consumption, investment, wages, hours worked, inflation, and interest rates). To model the housing sector in the manner of Iacoviello and Neri (2010) would require the addition of measures for capital and land.
Resources: poor. DSGE models are generally an advanced forecasting technique requiring specialised training and most likely the services of a PhD economist, especially during development. However, the required resources may not put DSGE models out of reach of the Scottish forecasting framework.
Our assessment of DSGE models is summarised in Appendix Table A7.
3.8 Microsimulation models and micro databases
Microsimulation models use survey data to construct a representative distribution of typical households and individuals in the economy. [35] Weights are then used to scale the sample to the population level. If linked to tax returns, microsimulation models can be used to assess the fiscal and distributional consequences of changes to the tax and transfer system.
Microsimulation models are not designed for forecasting-they are static accounting models that mechanically apply legislated or proposed tax and transfer parameters to the relevant characteristics of individuals and households. These may include characteristics such as an individual's net income, the number of children under a certain age that qualify for child benefits, or real estate purchases made throughout the year.
Certain properties of microsimulation models nonetheless allow them to be used as a tool in a wider framework to arrive at forecasts. Specifically, models can apply the current tax system to the population characteristics in past years. In this manner, forecasters can calculate the revenue elasticity (sensitivity of growth) of a tax to the tax base. For a flat tax, this revenue elasticity would be zero. However, for a graduated tax such as personal income taxes or LBTT, revenues will increase faster than one-to-one with the base. [36] This is known as fiscal drag. Because LBTT thresholds are not automatically indexed to inflation, fiscal drag could be significant.
The elasticity of revenues to the tax base can then be applied to a forecast of the tax base to arrive at a forecast of revenues. Although the model may be built with the ability to grow the base itself to future years, the benefit of this approach is that the forecast doesn't have to correspond exactly to the tax base of revenues. For example, the microsimulation-based elasticity can be imposed on a macroeconometric model by using its historical correlation with the National Accounts elasticity.
Although not technically a microsimulation model, some practitioners use a database of the universe of tax returns that can be queried to retrieve variables of interest. These can include simple relationships that can be programmatically changed and aggregated to cost alternative policies, or can be assessed before and after a policy has been implemented to assess its impact (for example, see Matthews (2016)).
Microsimulation models and micro databases are also among the few ways to examine the distribution of housing prices over time. If clear trends are observed in the summary statistics of the distribution (for example, its mean, variance, and symmetry), these may be forecast using techniques described above such as univariate time series models.
Assessment
Application (forecasting): poor. Microsimulation models and micro databases cannot, on their own, provide forecasts for the housing market. However, they can be used in conjunction with other forecast models to incorporate fiscal drag effects into the forecast. For example, their base years can be grown to future years by imposing growth rates from auxiliary forecast models, and tax rates and thresholds can then be applied to this uplifted base to project tax receipts.
Microsimulation models can be used to estimate variables to include in other models, such as multivariate econometric models. For example, microsimulation models can be used to calculate the average effective tax rates of homebuyers over history and the outlook to use as an explanatory variable when estimating the net benefits of home ownership.
Application (policy): good. Microsimulation models and micro databases are particularly well-suited for policy analysis. They are the main way that government budget authorities translate forecasts of the tax base into forecasts of revenues.
There are many examples of microsimulation models in the UK applied to policy analysis. HMRC has a microsimulation model specifically for SDLT that covers the universe of transactions. Other microsimulation models in the UK include the Department of Work and Pensions' Pensim2 model, the IFS's TAXBEN model, and the London School of Economics' SAGE model. However, these models don't have a detailed specification for SDLT or Scottish LBTT.
The OBR uses HMRC's residential stamp duty plus model ( SDM+) to prepare its devolved forecasts for Scottish residential LBTT, Stamp Duty Land Tax, and Welsh residential SDLT. OBR (2016) describes the SDM+ model as follows:
[ SDM+] allows us to apply the tax schedules for LBTT and SDLT to a full sample of transactions from a given year and then grow them in line with our price and transactions forecasts for the residential property markets (p. 22).
Microsimulation models are general developed for social policy analysis, personal income taxes, and consumption taxes. There are few microsimulation models applied to housing. [37]
Many studies assessing the behavioural response of UK policy measures simply use micro data files with the universe of tax returns to evaluate historical policy changes by looking at the period before and after the intervention. For example, Best and Klevin (2013) used the universe of SDLT administration data (that is, every property transaction) from 2004 to 2012 to assess a number of tax changes, including the success of the stamp duty holiday in 2008 to 2009 as fiscal stimulus. [38]
Microsimulation models are also useful for producing revenue sensitivity estimates, for example in the production of cyclically adjusted budget balanced and fan charts.
One drawback is that, because they are by nature mechanical, they require ad hoc adjustments to the simulation output to incorporate behavioural responses.
Accuracy. As the model itself cannot forecast, this criterion is not applicable. However, if economic variables forecast with auxiliary models are accurate, then the microsimulation model should give accurate conditional estimates of revenues.
Communication (story telling): good. Because microsimulation models are a rote imposition of the tax code on real households, communication of microsimulation results are intuitive.
Communication (transparency): good. The underlying equations are mechanical identities, and aside from weights to scale results to the population level, little estimation and no judgment is applied. Although model code can be a challenge to access and examine, results can typically be tested against back-of-the-envelope calculations.
Data compatibility: poor. There may be limitations to Scottish forecasters' access to tax-payer level data. Microsimulation model development may therefore only be possible if appropriate data protocols can be put in place.
Resources: poor . Microsimulation models require considerable resources to develop and maintain. The initial design requires a great deal of time and expertise on both tax policy and software development. However, the model may not need to be built from scratch. Li and O'Donoghue (2013) surveyed microsimulation models and point to four generic software programs that can be adapted to build new microsimulation models: ModGen (Wolfson and Rowe, 1998), UMDBS (Sauerbier, 2002), GENESIS (Edwards, 2004) and LIAM (O'Donoghue, Lennon, and Hynes, 2009).
Parameters need to be updated to reflect new tax and transfer legislation once or twice annually within the budget cycle. This can be an involved, resource-intensive process if policies are implemented that aren't simple rate or threshold changes.
Our assessment of the qualities of microsimulation models in relation to the Scottish budget forecast process is summarised in Appendix Table A8.
Contact
Email: Jamie Hamilton
Phone: 0300 244 4000 – Central Enquiry Unit
The Scottish Government
St Andrew's House
Regent Road
Edinburgh
EH1 3DG
There is a problem
Thanks for your feedback